As I began a new project that I wrote with static types, thanks to the typing module, baked into python 3.5, I noticed a bunch of new errors when it came to loading environmental constants.

Importing .env constants
Environmental constants are commonly stored in a .env file, and hold all sorts of values, for example database connection strings and private credentials for connecting to services, this is why they are usually added to your .gitignore file.
A good way to load environmental constants is with the PyPI library python-dotenv, it reads constants from a .env file, as long as they're formatted similarly to a bash file.
# demo .env file
string_example="I'm a string"
bool_example=false
int_example=123
float_example=0.29
import os
from dotenv import load_dotenv
load_dotenv()
# raw .env options
env_string_raw: str = os.environ.get("string_example")
env_bool_raw: bool = os.environ.get("bool_example")
env_int_raw: int = os.environ.get("int_example")
env_float_raw: int = os.environ.get("float_example")The first issue is these are all strings, dotenv hasn't detected the values for each item, it just assumes they're all strings, regardless of surrounding quotes or not.
Before I ran some more tests I created a function to analyse the constants vs what output I was expecting.
import os
from dotenv import load_dotenv
load_dotenv()
# make sure your environment file variables match below
CORRECT_VALUES = {
"str": "I'm a string",
"bool": False,
"int": 123,
"float": 0.29
}
def value_check(variable, variable_type, correct_values):
if variable == correct_values[variable_type] and type(variable) == type(
correct_values[variable_type]
):
print(f"{variable_type} variable matches type and value")
else:
print(
f"{variable_type} variable does not match value or type, {variable} {type(variable)} instead of {correct_values[variable_type]} {type(correct_values[variable_type])}"
)
# raw .env options
env_string_raw: str = os.environ.get("string_example")
env_bool_raw: bool = os.environ.get("bool_example")
env_int_raw: int = os.environ.get("int_example")
env_float_raw: int = os.environ.get("float_example")
print("---RAW ENV EXAMPLES---")
value_check(env_string_raw, "str", CORRECT_VALUES)
value_check(env_bool_raw, "bool", CORRECT_VALUES)
value_check(env_int_raw, "int", CORRECT_VALUES)
value_check(env_float_raw, "float", CORRECT_VALUES)
print()
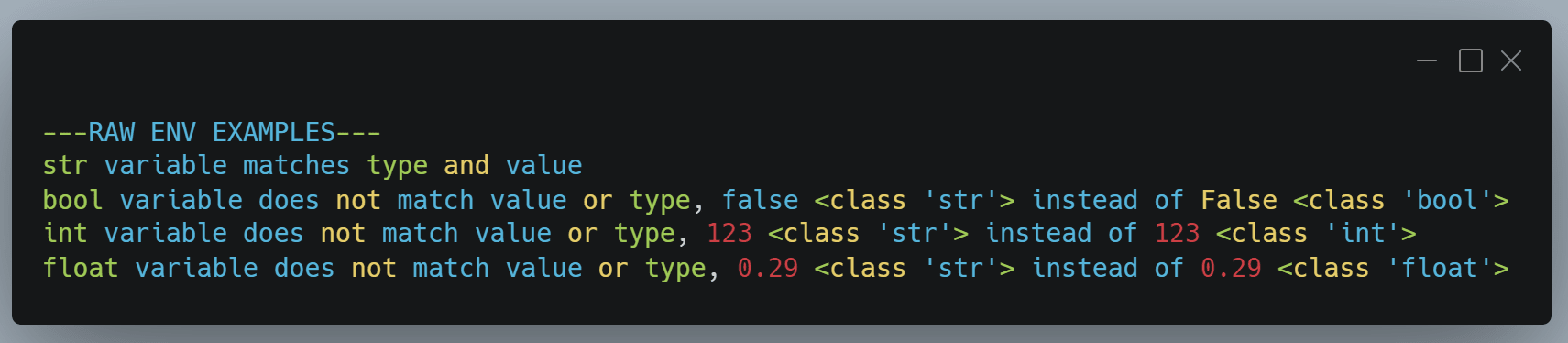
As the above output shows, only the string constant matches what I expect. So let's wrap each item in their proper type and see what returns.
# converted .env options
env_string: str = str(os.environ.get("string_example"))
env_bool: bool = bool(os.environ.get("bool_example"))
env_int: int = int(os.environ.get("int_example"))
env_float: float = float(os.environ.get("float_example"))
We managed to convert all values except for the bool one. We expect False, but the output is True. This is because anything that isn't an empty value eg. 0, "", None when converted to bool will be true. The string "false" (or "False") is not empty so the bool equivalent is True.
So to make this import method work with boolean values, I would have to make a custom function to manage bool imports, not what I want to be doing.
mypy typed code analysis
The next issue is typed code analysis. If I run the current code through mypy a static type linter, I get the following errors.
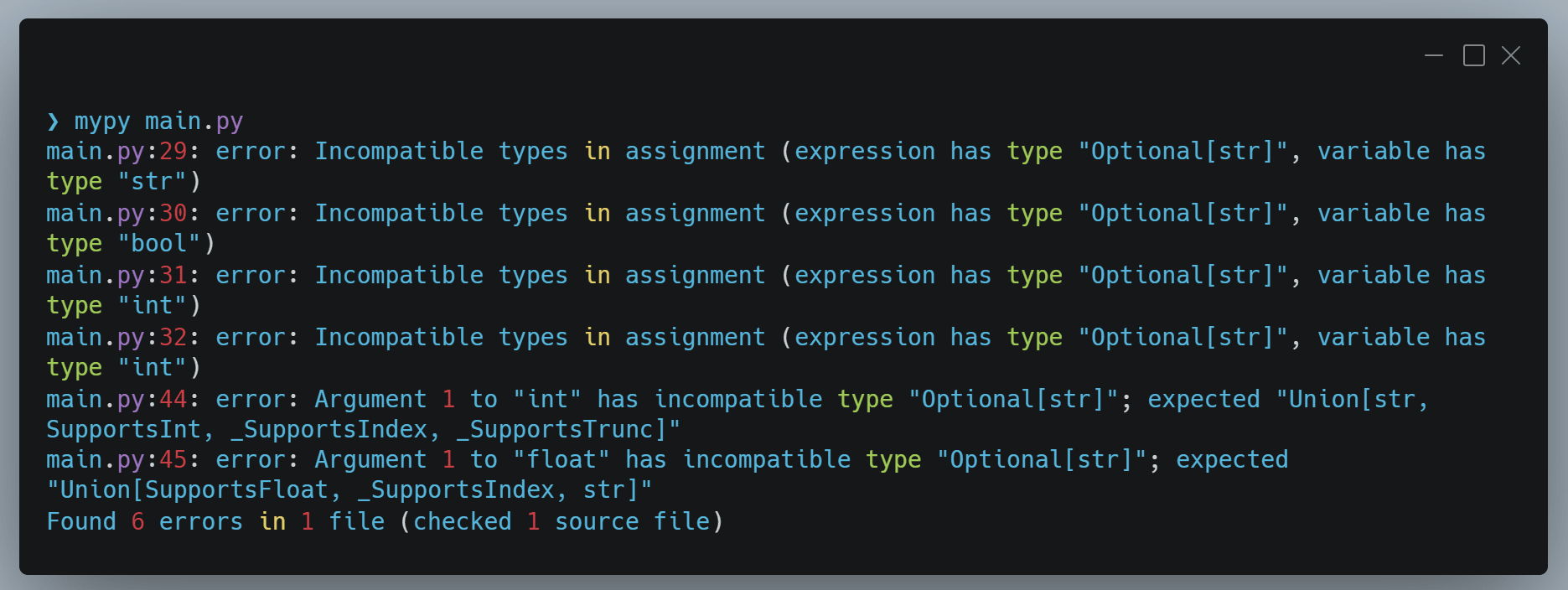
This output shows 6 errors, the first 4 relate to the initial 4 .env imports. They've all imported as a string, when expecting other types, and due to the nature of everything being a string with a dotenv import, mypy cannot assume any of the 4 values, including the actual string one, are meant to be a string.
mypy is also not happy about converting the types manually of the int and float constants in the converted examples. It knows I've had to convert these from strings, which is not ideal when trying to statically type my code.
Importing .env.toml constants
Enter toml. TOML is a another markup language format, similar to JSON and YAML, and like YAML it natively supports multiple types including - string, integer, float, boolean, date and time.
# example .env.toml file
[demo]
string_example = "I'm a string"
bool_example = false
int_example = 123
float_example = 0.29import toml
...
config = toml.load(".env.toml")
...
# toml options
toml_string: str = config["demo"]["string_example"]
toml_bool: bool = config["demo"]["bool_example"]
toml_int: int = config["demo"]["int_example"]
toml_float: float = config["demo"]["float_example"]
As you can see above, the toml environment file import values and types all match successfully, and mypy doesn't find any type lint errors with the variables.
TOML files make sense for environment files, especially if you want to progress with static typing in Python. I can't find a standard for naming them yet, so I've gone with .env.toml in my projects. Just remember to add this file to your .gitignore if you do the same.
You can find and download this code at https://github.com/mattwalshdev/demo-env_vs_toml
